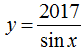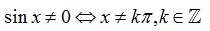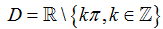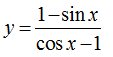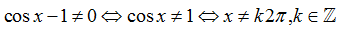Hàm số xác định khi nào? Cách các định hàm số ra sao?

Hàm số xác định khi nào? Tìm tập xác định của hàm số 11? Tìm tập xác định của hàm số 12? Tìm tập xác định của hàm số 10.

Bạn có còn nhớ kiến thức về hàm số hay không? Bạn có biết được hàm số xác định khi nào không? Đâu là cách để mà tìm tập xác định của hàm số bạn có biết hay không? Cùng tìm hiểu cách để xác định một hàm số thông qua những ví dụ trong bài viết này nhé.

Hàm số xác định khi nào

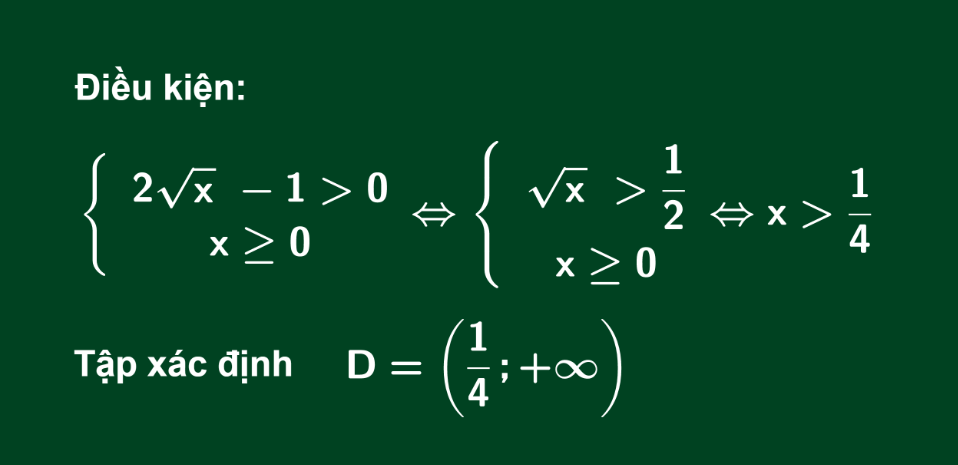
Hàm số xác định khi nào

Tập xác định của hàm số y=f(x) là tập con của R bao gồm các giá trị sao cho biểu thức f(x) xác định.

Ví dụ:

Số 3 không thuộc tập xác định của hàm số y=1/(x-3) vì khi ta thay số 3 vào biểu thức 1/(x-3) thì không tính được. Số 5 thuộc tập xác định vì khi thay số 5 vào ta tính được kết quả là 1/2. Rõ ràng đối với hàm số này chúng ta thấy có rất nhiều giá trị khác thuộc tập xác định. Chẳng hạn như: 1; 2; 4…

Vì vậy tìm tập xác định của hàm tức là tìm tất cả các giá trị của biến mà khi thay vào biểu thức của hàm ta tính được.

Tìm tập xác định của hàm số 10

Loại 1: Hàm không chứa căn và không chứa mẫu thì tập xác định là R. Ví dụ như hàm số bậc nhất y=ax+b và hàm số bậc 2 y=ax²+bx+c (a≠0) là các hàm có tập xác định là R.

Loại 2: Hàm số chứa ẩn dưới mẫu thì mẫu cần khác 0.

Ví dụ:

Tìm tập xác định của hàm sau:

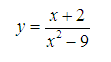
Lời giải:

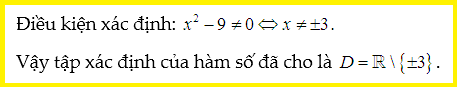
Loại 3: Hàm số chứa ẩn trong căn bậc chẵn thì trong căn phải lớn hơn hoặc bằng 0 (Căn không dưới mẫu) hoặc trong căn lớn hơn hẳn 0 (Căn dưới mẫu).

Ví dụ:

Tìm tập xác định của hàm sau:

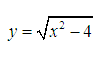
Lời giải:

Nhận xét: Đây là trường hợp căn không dưới mẫu.

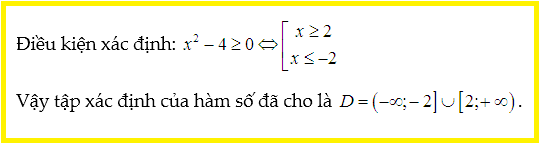
Ví dụ: 

Tìm tập xác định của hàm sau:

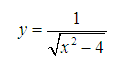
Lời giải:

Nhận xét: Đây là trường hợp căn dưới mẫu. Tác giả chọn biểu thức gần với ví dụ trên để các em học sinh tiện so sánh.

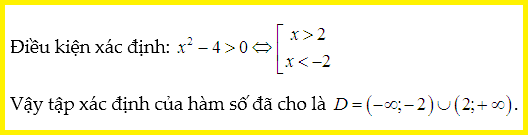
Chú ý: Trong một hàm mà có chứa nhiều loại như đã  nêu ở trên. Bởi vì chúng ta cần tất cả các điều kiện phải xác định nên ta cần viết tất cả các điều kiện và phải đặt trong dấu hệ.

Ví dụ:

Tìm tập xác định của hàm sau:

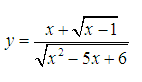
Lời giải:

Tìm tập xác định của hàm số 11

Hàm số y = 1/f(x) xác định khi f(x) ≠ 0 .

+ Hàm số y= √(f(x)) xác định khi f(x) ≥ 0.

+ Hàm số y = 1/√(f(x)) xác định khi f(x)> 0

+ Hàm số y= tan [f(x)] xác định khi cos[f(x)] ≠ 0 .

+ Hàm số y = cot [f(x)] xác định khi sin[ f(x)] ≠ 0

+ Hàm số y= tan[ f(x)]+cot⁡[g(x)] xác định khi cos⁡[f(x)] ≠ 0;sin⁡[ g(x)] ≠ 0

* Chú ý:

sinx ≠ 0 ⇔ x ≠ k.π

cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên

sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π

cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π

Ví dụ minh họa

Ví dụ 1. Tìm tập xác định D của hàm số 

Lời giải:

Hàm số xác định khi và chỉ khi 

Vậy tập xác định 

Ví dụ 2. Tìm tập xác định D của hàm số 

Lời giải:

Hàm số xác định khi và chỉ khi 

Vậy tập xác định  .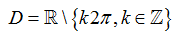

Tìm tập xác định của hàm số 12

Hàm số y = 1/f(x) xác định khi f(x) ≠ 0 .

+ Hàm số y= √(f(x)) xác định khi f(x) ≥ 0.

+ Hàm số y = 1/√(f(x)) xác định khi f(x)> 0

+ Hàm số y= tan [f(x)] xác định khi cos[f(x)] ≠ 0 .

+ Hàm số y = cot [f(x)] xác định khi sin[ f(x)] ≠ 0

+ Hàm số y= tan[ f(x)]+cot⁡[g(x)] xác định khi cos⁡[f(x)] ≠ 0;sin⁡[ g(x)] ≠ 0

* Chú ý:

sinx ≠ 0 ⇔ x ≠ k.π

cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên

sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π

cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π

Ví dụ minh họa

Ví dụ 1. Tìm tập xác định D của hàm số 

Lời giải:

Hàm số xác định khi và chỉ khi 

Vậy tập xác định 

Ví dụ 2. Tìm tập xác định D của hàm số 

Lời giải:

Hàm số xác định khi và chỉ khi 

Vậy tập xác định  .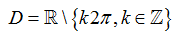

Ví dụ 3. Tập xác định của hàm số 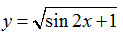 . là

Lời giải:

Ta có  .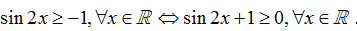

Vậy hàm số đã cho xác định với mọi x∈R

Ví dụ 4. Hàm số 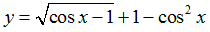 chỉ xác định khi:

Lời giải:

Hàm số đã cho xác định khi cos x – 1 ≥0, mà cos x – 1 ≤0,∀x∈R

Do vậy để hàm số xác định thì cosx=1, x= k2π,k∈Z

Ví dụ 5. Tập xác định của hàm số 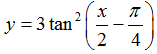 là:

Lời giải:

Hàm số xác định khi cos⁡(x/2-π/4) ≠ 0

⇔ x/2-π/4  ≠  π/2+kπ ⇔ x/2  ≠  3π/4+kπ

⇔ x  ≠  3π/2+k2π,k ∈ Z

Ví dụ 6: Tập xác định của hàm số D.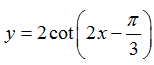 . là:

Lời giải:

Hàm số xác định khi sin⁡(2x-π/3) ≠ 0

⇔2x-π/3 ≠  kπ ⇔ 2x  ≠  π/3+ kπ

⇔ x  ≠  π/6+kπ/2,k ∈ Z

Vậy là bạn đã có được đáp án cho thắc mắc hàm số xác định khi nào sau khi đọc bài viết này rồi đúng không nào? Bạn có thấy rằng những thông tin này thú vị hay không? Nếu câu trả lời là có nhớ sẻ chia cho mọi người nhé. Như thế những ai cần có thể ôn tập lại kiến thức về hàm số ấy bạn à.

• Xem thêm: Uống sâm alipas bao lâu thì có tác dụng cũng như hiệu quả?

• Fitter nghĩa là gì? Được sử dụng như thế nào bạn có biết?

• Kích thước vios như thế nào? So với xe cùng phân khúc ra sao

• Kích thước banner shopee ra làm sao? Có phù hợp không?

• Bị ho có nên ăn mì tôm không? Nếu ăn thì có làm sao không?

• Oppo a54 ra mắt khi nào? Có nên dùng điện thoại này không?

• Uống sâm alipas bao lâu thì có tác dụng cũng như hiệu quả?

• Trong nguồn điện lực lạ có tác dụng như thế nào bạn có biết?